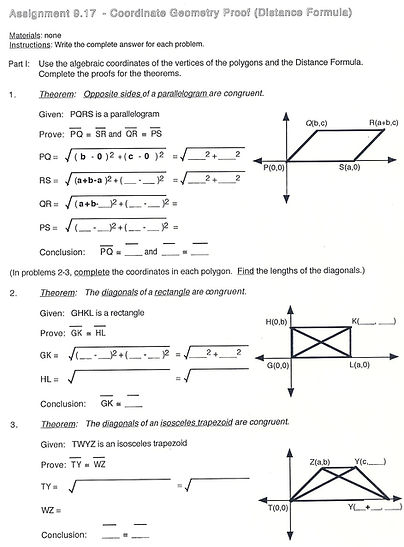
​Coordinate Geometry Proof (Distance Formula)

About Geometry Worksheet Assignment 9.17:                   

 

Assignment 9.17 is an introduction to using the Distance formula to complete algebraic proofs of geometry theorems about lengths of segments in certain triangles and quadrilaterals.

 

Prerequisite Skills:  Find the algebraic expression for the distance between two points having algebraic coordinates (Assignment 9.11).  Write algebraic coordinates for vertices and midpoints of sides of certain triangles and quadrilaterals (Assignment 9.16).  

 

Theorems:  The opposite sides of a parallelogram are congruent.

                           The diagonals of a rectangle are congruent.

                           The diagonals​ of an isosceles trapezoid are congruent.

                           The midpoint of the hypotenuse of a right triangle is equidistant from the vertices of the triangle.

                           The medians​ to the legs of an isosceles triangle are congruent.

                           The quadrilateral made of line segments with endpoints of the midpoints of consecutive sides of a rectangle is a rhombus.