
where students teach themselves
A comprehensive geometry curriculum
Geometry for School and Home
Activity 3.8
Assignment 3.9
Previous
Next
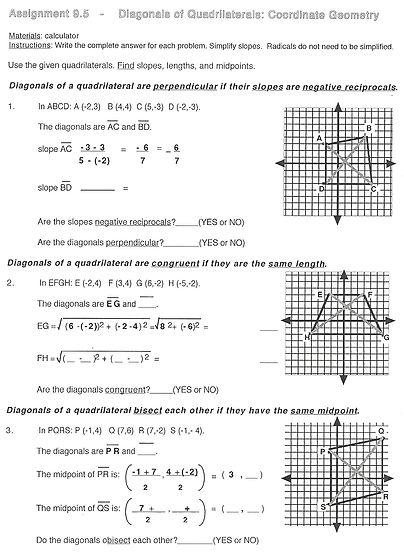
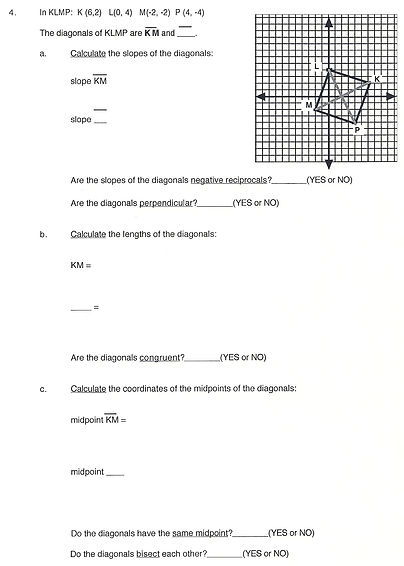
Assignment 9.5
Diagonals of Quadrilaterals: Coordinate Geometry
Objective
Use slope and the Distance Formula to determine if diagonals of quadrilaterals are congruent, perpendicular, or bisect each other.
About Geometry Worksheet Assignment 9.5:
Assignment 9.5 is an introduction to using both the Distance and slope formulas in determining the relationships of diagonals of quadrilaterals.
Prerequisite Skills: Find the distance between two points using the Distance formula (Assignment 9.2). Find the slope of a line through two points (Assignment 1.8). Use slopes to determine whether lines are perpendicular (Assignment 2.18). Find the coordinates of the midpoint of a line segment (Assignment 1.17).
Theorems: Diagonals of quadrilaterals are perpendicular if their slopes are negative reciprocals.
Diagonals of quadrilaterals are congruent if they have the same length.
Diagonals of quadrilaterals bisect each other if they have the same midpoint.